Log loss

Introduction

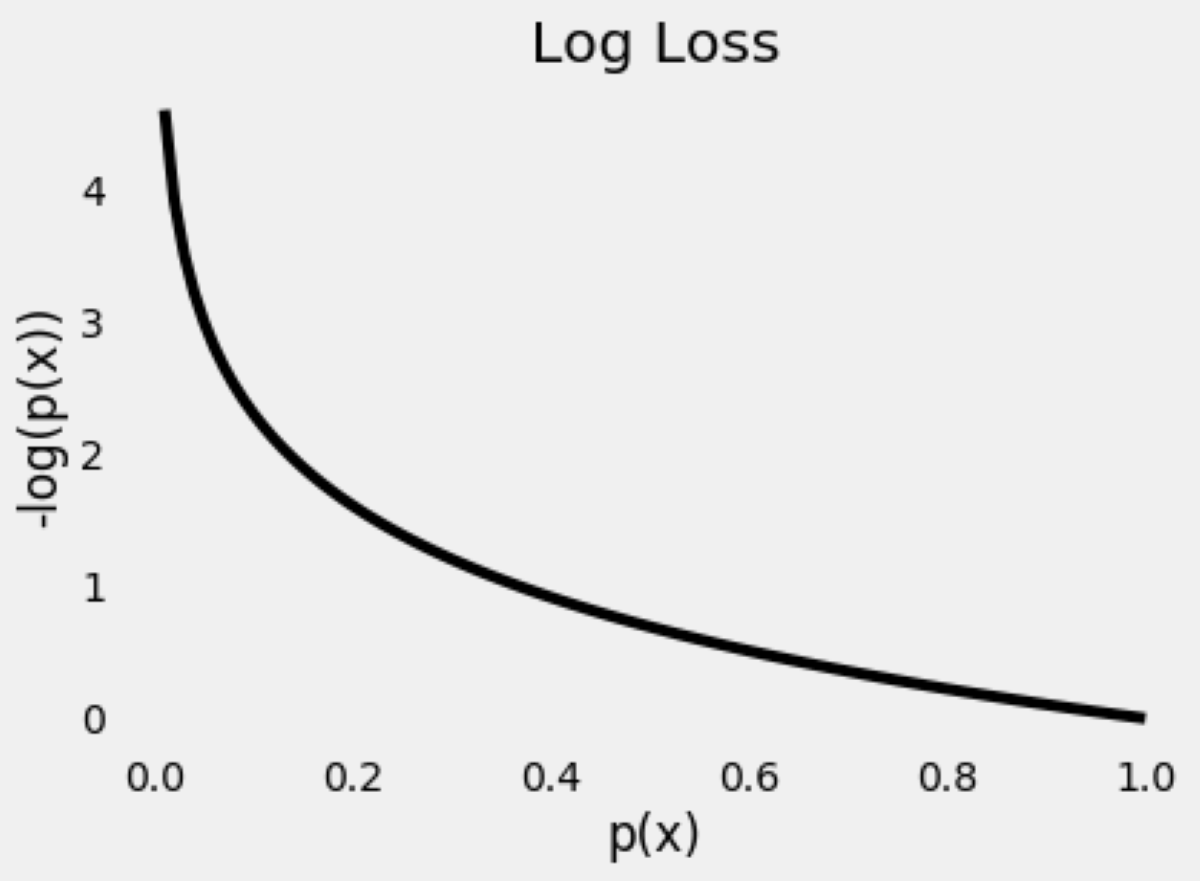
Log loss is a metric where a lower value equates to better performing model, it is a slight variation on something called the "Likelihood" Function, let's start there.

Likelihood

A car dealer, and is trying to sell 3 cars, he trains a machine learning model to predict whether they'll be sold or not based on current market conditions. Here what happened 👇

The model gives a probabilty that the car would be sold or not. Then we have ground truth, which is what actually happened, either it got sold or it didn't denoted by 0% or 100%.

Likelihood is how "correct" the model or how close it was to the ground truth.

Let us understand this in each case, starting with the Tesla. The model was 80% sure that and the rest 20% that it wouldn't and groundtruth was that it actually ended up selling.

Which the model was 80% (0.8) correct.

Similarly in the case of the BMW it was 40% sure it would be sold and 60% that it wouldn't and groundtruth was that it actually ended up selling.

Which means in this case the model was 40% (0.4) correct.

Lastly in the case of the Mercedes, the model thought it would sell with a 10% probability and 90% that it wouldn't and groundtruth was that it actually ended up NOT selling.

Which means in this case the model was 90% (0.9) correct.

In order to find the likelihood, we multiply these values 0.9 x 0.4 x 0.8 = 0.288 and that is the likelihood.

What we're trying to find out here is how well the model lines up with the groundtruth, but there's a problem with this metric.

In this case we just had 3 scenarios but in most real life situations, there are hundreds or even thousands of these and the thing with that is the value of likelihood decreases as more and more cases are added as it can also be observed in the above example.

This makes it incredibly difficult for the computer to caclulate the likelihood, we can solve this issue by using a modified likelihood metric : Log loss.

Log Loss

Log loss is essentially the log of the likelihood multiplied by -1, this is a simple computational trick that keeps the value in a range that the computer can calculate. As a result of these transformations, the lesser the value of the log loss, the better the model.